题目内容
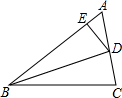 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.分析:过点D作DF⊥BC于F,根据角平分线上的点到角的两边的距离相等可得DE=DF,然后根据三角形的面积列出方程求解即可.
解答: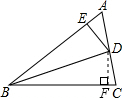 解:如图,过点D作DF⊥BC于F,
解:如图,过点D作DF⊥BC于F,
∵BD是∠ABC的平分线,DE⊥AB,
∴DE=DF,
∴S△ABC=
AB•DE+
BC•DF=90,
即
×18•DE+
×12•DE=90,
解得DE=6.
 解:如图,过点D作DF⊥BC于F,
解:如图,过点D作DF⊥BC于F,∵BD是∠ABC的平分线,DE⊥AB,
∴DE=DF,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得DE=6.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,三角形的面积,熟记性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD= 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是