题目内容
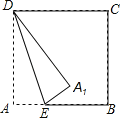
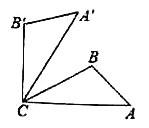
【题目】如图，将
绕点
按逆时针方向旋转
后得到
，若
，
，且
，则
，
两点之间的距离为（ ）
A.
B.
C.2D.
【答案】A
【解析】
利用三角形内角和定理求出∠A′CB′=30°，然后利用旋转的性质得到BC=B′C，再利用全等三角形的判定和性质得到A′B=A′B′进而求出此题的答案．
解：如图，连接A′BA′B．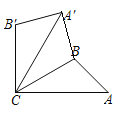
∵∠A=45°，∠B'=105°，
∴∠A′CB′=180°45°105°=30°，
∵将△ABC绕点C按逆时针方向旋转60°后得到△A'B'C，
∴∠B′CB=60°，AB=A′B′=
，
∴∠A′CB=60°30°=30°，
∴∠A′CB′=∠A′CB，
在△A′B′C和△A′BC中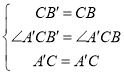
,
∴△A′B′C≌△A′BC，
∴A′B′=A′B=，
故选A．
【题目】疫情期间，甲厂欲购买某种无纺布生产口罩，A、B两家无纺布公司各自给出了该种无纺布的销售方案．
A公司方案：无纺布的价格均为每吨1.95万元
；
B公司方案：无纺布不超过30吨时，每吨收费2万元；超过30吨时，超过的部分每吨收费1.9万元．
设甲厂在同一公司一次购买无纺布的数量为x吨（x>0）．
（Ⅰ）根据题意，填写下表：
一次购买数量（吨） | 10 | 20 | 35 | … |
A公司花费（万元） | 39 | … | ||
B公司花费（万元） | 40 | … |
（Ⅱ） 设在A公司花费
万元，在B公司花费
万元，分别求、关于x的函数解析式；
（Ⅲ）如果甲厂所需购买的无纺布是50吨，试通过计算说明选择哪家公司费用较少．
【题目】某服装公司有
型童装80件，
型童装120件，分配给下属的“万达”和“万象城”两个专卖店销售，其中140件给万达店，60件给万象城店，且都能卖完，两商店销售这两种童装每件的利润（元）如表：
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
（1）设分配给万达店型产品
件（
），请在下表中用含的代数式填写：
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为
（元），求关于的函数关系．
（2）现要求总利润不低于18140元，请说明有多少种不同分配方案，并写出各种分配方案．
