题目内容
如图,O为正方形ABCD的对角线AC与BD的交点,M、N两点分别在BC与AB上,且OM⊥ON.
(1)试说明OM=ON;
(2)试判断CN与DM的关系,并加以证明.

(1)试说明OM=ON;
(2)试判断CN与DM的关系,并加以证明.

(1)∵四边形ABCD是正方形,
∵OC=OB,∠OCM=∠OBN=45°,BD⊥AC,
∵OM⊥ON,
∴∠MON=∠COB=90°,
∴∠MON-∠MOB=∠COD-∠MOB,
∴∠COM=∠BON,
∵在△ONB和△OMC中,
∴△ONB≌△OMC(ASA),
∴OM=ON.
(2)CN=DM,CN⊥DM,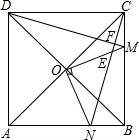
证明:∵四边形ABCD是正方形,
∴OC=OD,BD⊥AC,
∴∠DOC=∠BOC=90°,
∵∠COM=∠BON,
∴∠DOC+∠COM=∠BOC+∠BON,
即∠DOM=∠CON,
∵在△DOM和△CON中
∴△DOM≌△CON(SAS),
∴CN=DM,∠DMO=∠CNO,
∵∠MON=90°,
∴∠NEO+∠CNO=90°,
∵∠MEC=∠NEO,
∴∠DMO+∠MEC=90°,
∴∠MFE=180°-90°=90°,
∴CN⊥DM.
∵OC=OB,∠OCM=∠OBN=45°,BD⊥AC,
∵OM⊥ON,
∴∠MON=∠COB=90°,
∴∠MON-∠MOB=∠COD-∠MOB,
∴∠COM=∠BON,
∵在△ONB和△OMC中,
|
∴△ONB≌△OMC(ASA),
∴OM=ON.
(2)CN=DM,CN⊥DM,

证明:∵四边形ABCD是正方形,
∴OC=OD,BD⊥AC,
∴∠DOC=∠BOC=90°,
∵∠COM=∠BON,
∴∠DOC+∠COM=∠BOC+∠BON,
即∠DOM=∠CON,
∵在△DOM和△CON中
|
∴△DOM≌△CON(SAS),
∴CN=DM,∠DMO=∠CNO,
∵∠MON=90°,
∴∠NEO+∠CNO=90°,
∵∠MEC=∠NEO,
∴∠DMO+∠MEC=90°,
∴∠MFE=180°-90°=90°,
∴CN⊥DM.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
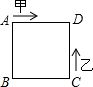
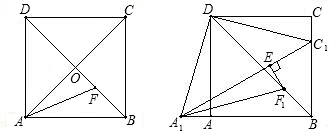



 顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.