题目内容
【题目】如图，点A在反比例函数y=
（x＞0）的图像上，点B在反比例函数y=
（x＞0）的图像上，AB∥x轴，BC⊥x轴，垂足为C，连接AC，若△ABC的面积是6，则k的值为（ ）
A. 10 B. 12 C. 14 D. 16
【答案】D
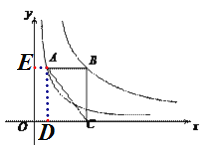
【解析】分析：作AD⊥x轴于点D，作AE⊥y轴于点E，由△ABC的面积是6，可得矩形ABCD的面积是12，然后根据S矩形ADOE+S矩形ABCD=S矩形BCOE，即可求出k的值.
详解： 作AD⊥x轴于点D，作AE⊥y轴于点E.
∵△ABC的面积是6，
∴矩形ABCD的面积是12，
∵S矩形ADOE+S矩形ABCD=S矩形BCOE，
∴4+12=
，
∵反比例函数y=
（x＞0）的图像在一、三象限，
∴k>0，
∴k=16.
故选D.
练习册系列答案
相关题目
