题目内容
如图,AB=2,BC=5,AB⊥BC与B,l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q。

求证:∠A=∠QPC
当点P运动到何处时,PA=PQ?并说明理由。

求证:∠A=∠QPC
当点P运动到何处时,PA=PQ?并说明理由。
在直角三角形ABP中,∠APB+∠A=90°,又因为∠APB+∠QPC=90°,所以∠A=∠QPC。当P运动到离C处距离为2时,PA=PQ 理由:当PC=AB=2时,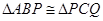 ,此时PA=PQ
,此时PA=PQ
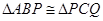 ,此时PA=PQ
,此时PA=PQ试题分析:在直角三角形ABP中,∠APB+∠A=90°,又因为∠APB+∠QPC=90°,所以∠A=∠QPC。当P运动到离C处距离为2时,PA=PQ
理由:当PC=AB=2时,
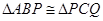 ,此时PA=PQ
,此时PA=PQ点评:本题难度较低,主要考查学生对直角三角形性质和全等三角形性质知识点的掌握。为中考常考题型,学生要牢固掌握。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
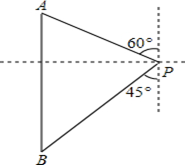
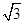 的斜坡笔直滑下,若下滑的垂直高度为1000 米.则这名运动员滑到坡底的路程是 米.
的斜坡笔直滑下,若下滑的垂直高度为1000 米.则这名运动员滑到坡底的路程是 米.
 的直角三角板测量树高,已知小聪和树都与地面垂直,且相距
的直角三角板测量树高,已知小聪和树都与地面垂直,且相距 米,小聪身高AB为1.7米,则这棵树的高度= 米
米,小聪身高AB为1.7米,则这棵树的高度= 米
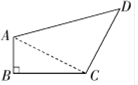

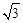 ,BC=2,则tanB= ;
,BC=2,则tanB= ;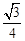 ,则锐角α= 度.
,则锐角α= 度.