Question

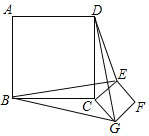
【题目】如图，正方形ABCD和正方形CEFG边长分别为a和b，正方形CEFG绕点C旋转，给出下列结论：①BE＝DG；②BE⊥DG；③DE2+BG2＝2a2+b2，其中正确结论是_____(填序号)

Answer 1

【答案】①②

【解析】

由四边形ABCD与四边形EFGC都为正方形，得到四条边相等，四个角为直角，利用SAS得到三角形BCE与三角形DCG全等，利用全等三角形对应边相等即可得到BE＝DG，利用全等三角形对应角相等得到∠1＝∠2，利用等角的余角相等及直角的定义得到∠BOD为直角，利用勾股定理求出所求式子的值即可.

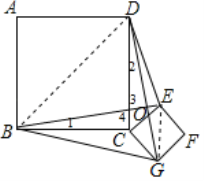
如图，设BE，DG交于O，

∵四边形ABCD和EFGC都为正方形，

∴BC＝CD，CE＝CG，∠BCD＝∠ECG＝90°，

∴∠BCE+∠DCE＝∠ECG+∠DCE＝90°+∠DCE，即∠BCE＝∠DCG，

在△BCE和△DCG中，，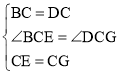

∴△BCE≌△DCG(SAS)，

∴∠1＝∠2，BE＝DG，故①正确，

∵∠3=∠4，∠BCD=90°，

∴∠1+∠4＝∠3+∠2＝90°，

∴∠BOD＝90°，

∴BE⊥DG；故②正确；

如图，连接BD，EG，

∴DO2+BO2＝BD2＝BC2+CD2＝2a2，EO2+OG2＝EG2＝CG2+CE2＝2b2，

∴BG2+DE2＝OG2+BO2+EO2+ DO2＝2a2+2b2，故③错误.

故答案为：①②.