ĢāÄæÄŚČŻ
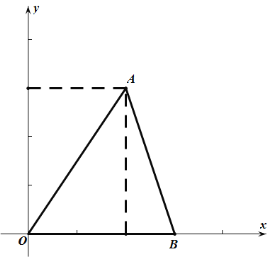
”¾ĢāÄæ”æŗĆɽŗĆĖ®ŗĆ½É½£¬ŹÆ¹°ĒÅŌŚ½É½“¦“¦æɼū£¬Š”Ć÷ŅŖ°ļƦ“¬·ņ¼ĘĖćŅ»ĖŅ»õ“¬ŹĒ·ńÄܹ»°²Č«ĶعżŅ»×łŌ²»”ŠĪµÄ¹°ĒÅ£¬ĻÖ²āµĆĒÅĻĀĖ®Ćęæķ¶Č16mŹ±£¬¹°¶„øß³öĖ®Ę½ Ćę4m£¬»õ“¬æķ12m£¬“¬²Õ¶„²æĪŖ¾ŲŠĪ²¢øß³öĖ®Ćę3m”£
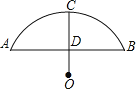
£Ø1£©ĒėÄć°ļÖśŠ”Ć÷Ēó“ĖŌ²»”ŠĪ¹°Ēŵİė¾¶£»
£Ø2£©Š”Ć÷ŌŚ½ā¾öÕāøöĪŹĢāŹ±Óöµ½Ą§ÄŃ£¬ĒėÄćÅŠ¶ĻŅ»ĻĀ£¬“Ė»õ“¬ÄÜĖ³ĄūĶعżÕā׳¹°ĒÅĀš£æĖµĖµÄćµÄĄķÓÉ.
”¾“š°ø”æ£Ø1£©“ĖŌ²»”ŠĪ¹°Ēŵİė¾¶ĪŖ10m£»£Ø2£©“Ė»õ“¬ÄÜĖ³Ąū²»ÄÜĶعżÕā׳¹°ĒÅ.ĄķÓɼū½āĪö.
”¾½āĪö”æ
£Ø1£©Į¬½ÓOA£¬ĄūÓĆ“¹¾¶¶ØĄķŗĶ¹“¹É¶ØĄķ¹¹Ōģ·½³Ģ£¬Ēó³ö¹°Ēŵİė¾¶³¤£»
£Ø2£©ČēĶ¼£¬EF³¤ĪŖ12Ć׏±£¬ĶعżĒó¾ąĄėĖ®Ćęø߶ČDGµÄ³¤Óė»õ“¬¶„²æµÄ3Ć××ö±Č½ĻĄ“ÅŠ¶Ø»õ“¬ÄÜ·ńĶعż£®ĻČøł¾Ż°ėĻŅFG£¬°ė¾¶ŗĶĻŅŠÄ¾ąOG¹¹ŌģÖ±½ĒČż½ĒŠĪĒó³öOGµÄ³¤Ą“ÅŠ¶Ļ£®
£Ø1£©½ā£ŗĮ¬½ÓOA£¬

ÓÉĢāŅāæÉÖŖCD=4£¬AB=16£¬OC”ĶABÓŚµćD£¬
”ą![]() ,
,
ÉčOA=r£¬ŌņOD=r-4
”ą£Ør-4£©2+82=r2 £¬
½āÖ®£ŗr=10
“š£ŗ“ĖŌ²»”ŠĪ¹°Ēŵİė¾¶ĪŖ10m.
£Ø2£©½ā£ŗČēĶ¼

ӧEF=12
”ąFG=12”Ā2=6
”ąOG=![]()
ӧOD=10-4=6
”ąDG=OG-OD=8-6=2£¼3
”ą“Ė»õ“¬ÄÜĖ³Ąū²»ÄÜĶعżÕā׳¹°ĒÅ.

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø”¾ĢāÄæ”æ»ł“”ÖŖŹ¶æ¼²é£ŗ
£Ø1£©Ņ»“ĪŗÆŹż±ķ“ļŹ½ £¬µ±k>0£¬b>0Ź±£¬Ķ¼Ļń¾¹ż ĻóĻŽ£»µ±k>0£¬b<0Ź±£¬Ķ¼Ļń¾¹ż ĻóĻŽ£»µ±k<0£¬b>0Ź±£¬Ķ¼Ļń¾¹ż ĻóĻŽ£»µ±k<0£¬b<0Ź±£¬Ķ¼Ļń¾¹ż ĻóĻŽ£®ĢŲ±šµ±b=0Ź±£¬Ķ¼Ļń¾¹ż £¬³ĘĪŖ ŗÆŹż£®
£Ø2£©·“±ČĄżŗÆŹżČżÖÖ±ķ“ļ·½Ź½·Ö±šĪŖ£ŗ ”¢ ”¢ ·“±ČĄżŗÆŹżµÄĶ¼Ļń³ĘĪŖ £¬µ±k>0Ź±£¬Ķ¼ĻńŌŚ ŗĶ ĻóĻŽ£¬yĖęxµÄŌö“ó¶ų £»µ±k<0Ź±£¬Ķ¼ĻńŌŚ ŗĶ ĻóĻŽ£¬yĖęxµÄŌö“ó¶ų £®
£Ø3£©ĢŲŹāČż½ĒŗÆŹżÖµ£ŗ
0”ć | 30”ć | 45”ć | 60”ć | 90”ć | |
sinA | |||||
cosA | |||||
tanA | |||||
cotA |
£Ø4£©¶ž“ĪŗÆŹż±ķ“ļŹ½£ŗ
¢ŁŅ»°ćŹ½£ŗ £»
¢Ś¶„µćŹ½£ŗ £» £» £»
£®
¢Ū½»µćŹ½£ØµćŹ½£©£ŗ £»
¢Ü¶Ō³ĘÖį¹«Ź½£ŗ ¶„µć×ų±ź¹«Ź½£ŗ £®
¢Ż¶ž“ĪŗÆŹżĶ¼Ļń³ĘĪŖ £¬µ±a>0Ź±£¬Ķ¼ĻńæŖæŚĻņ £»µ±a<0Ź±£¬Ķ¼ĻńæŖæŚĻņ £®c>0Ź±£¬Ķ¼ĻńŗĶ ÖįÕż°ėÖįĻą½»£¬c<0Ź±£¬Ķ¼ĻńŗĶ Öįøŗ°ėÖįĻą½»£®