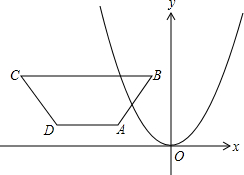
题目内容
11、写出抛物线y=x2+3x-4与抛物线y=-x2-2x+3的两个共同点
与x轴都有两个交点,都过(1,0)等
分析:两个抛物线的对称轴不同,开口方向相反,与y轴的交点坐标不同,可考虑两个抛物线与x轴的交点情况.
解答:解:∵y=x2+3x-4=(x+4)(x-1),
y=-x2-2x+3=-(x+3)(x-1),
∴这两条抛物线的共同点是两条抛物线与x轴都有两个交点,都过(1,0)点.
故答案为与x轴都有两个交点,都过(1,0)点.
y=-x2-2x+3=-(x+3)(x-1),
∴这两条抛物线的共同点是两条抛物线与x轴都有两个交点,都过(1,0)点.
故答案为与x轴都有两个交点,都过(1,0)点.
点评:本题考查了二次函数的性质.研究二次函数的性质,可以从开口方向,对称轴,顶点坐标,与x轴、y轴的交点坐标,增减性等方面进行探讨.

练习册系列答案
相关题目