题目内容
如图,在直角坐标系内,已知等腰梯形ABCD,AD∥BC∥x轴,AB=CD,AD=2,BC=8,AB=5,B点的坐标是(-1,5).(1)直接写出下列各点坐标.A(,)C(,)D(,);
(2)等腰梯形ABCD绕直线BC旋转一周形成的几何体的表面积(保留π);
(3)直接写出抛物线y=x2左右平移后,经过点A的函数关系式;
(4)若抛物线y=x2可以上下左右平移后,能否使得A,B,C,D四点都在抛物线上?若能,请说理由;若不能,将“抛物线y=x2”改为“抛物线y=mx2”,试确定m的值,使得抛物线y=mx2经过上下左右平移后能同时经过A,B,C,D四点.
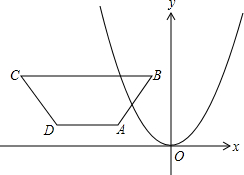
分析:(1)易得点C的纵坐标和点B的纵坐标相等,横坐标比点B的横坐标小8,过A作AE⊥BC于点E,那么BE=3,利用勾股定理可得AE=4,那么点A的横坐标比点B的横坐标小3,纵坐标比点B纵坐标小4,点D的纵坐标和点A的纵坐标相等,横坐标比点A的横坐标小2;
(2)绕直线BC旋转一周形成的几何体的表面积为两个底面半径为4,母线长为5的圆锥的侧面积和一个半径长为4,母线长为2的圆柱的侧面的和,把相关数值代入即可求解;
(3)设新函数解析式为y=(x-h)2,把(-4,1)代入即可求解;
(4)可把等腰梯形以y轴为对称轴放在平面直角坐标系中,确定一点,看其余点是否在y=x2上;进而设函数的解析式为y=mx2,A,B中的2点代入即可求解.
(2)绕直线BC旋转一周形成的几何体的表面积为两个底面半径为4,母线长为5的圆锥的侧面积和一个半径长为4,母线长为2的圆柱的侧面的和,把相关数值代入即可求解;
(3)设新函数解析式为y=(x-h)2,把(-4,1)代入即可求解;
(4)可把等腰梯形以y轴为对称轴放在平面直角坐标系中,确定一点,看其余点是否在y=x2上;进而设函数的解析式为y=mx2,A,B中的2点代入即可求解.
解答: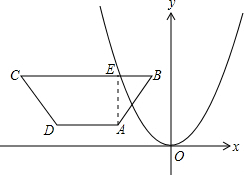 解:(1)A(-4,1);C(-9,5);D(-6,1);
解:(1)A(-4,1);C(-9,5);D(-6,1);
(2)形成的几何体的表面积为:2π×4×5+2π×4×2=56π;
(3)设所求的函数解析式为y=(x-h)2,
∴(-4-h)2=1,
h=-5或-3,
∴y=(x+5)2,y=(x+3)2;
(4)把等腰梯形以y轴为对称轴放在平面直角坐标系中,点A的横坐标为1,纵坐标为1,那么点B的坐标为(4,5),不在y=x2上,所以无论如何平移,都不能使得A,B,C,D四点都在抛物线上;
设y=mx2,点A(1,a),点B(4,a+4),
∴m=a,16m=a+4,
解得m=
,
∴y=
x2.
 解:(1)A(-4,1);C(-9,5);D(-6,1);
解:(1)A(-4,1);C(-9,5);D(-6,1);(2)形成的几何体的表面积为:2π×4×5+2π×4×2=56π;
(3)设所求的函数解析式为y=(x-h)2,
∴(-4-h)2=1,
h=-5或-3,
∴y=(x+5)2,y=(x+3)2;
(4)把等腰梯形以y轴为对称轴放在平面直角坐标系中,点A的横坐标为1,纵坐标为1,那么点B的坐标为(4,5),不在y=x2上,所以无论如何平移,都不能使得A,B,C,D四点都在抛物线上;
设y=mx2,点A(1,a),点B(4,a+4),
∴m=a,16m=a+4,
解得m=
| 4 |
| 15 |
∴y=
| 4 |
| 15 |
点评:平行于x轴的直线上的点的纵坐标相等;抛物线的平移,二次项的系数不变,只看顶点的平移即可;抛物线经过各点,那么各点的坐标应适合这个函数解析式.

练习册系列答案
相关题目
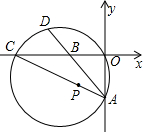 AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.
AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.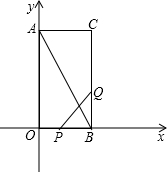
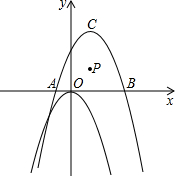 (2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
(2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2. 如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.
如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.