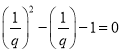题目内容
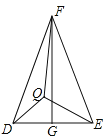
【题目】如图,在等腰△DEF中,DF=EF,FG是△DEF的中线,若点Q为△DEF内一点且Q满足∠QDF=∠QED=∠QFE,FQ=9,![]() =
=![]() ,则DQ+EQ=( )
,则DQ+EQ=( )
A.10B.![]() C.6+6
C.6+6![]() D.7
D.7![]()
【答案】A
【解析】
由等腰三角形的性质和勾股定理可表示出EF的长,通过证明△DQE∽△EQF,可得 ![]() ,即可求解.
,即可求解.
∵DF=EF,FG是△DEF的中线,
∴DG=GE,FG⊥DE,∠FDE=∠FED,
∵![]() ,
,
∴设DE=x,则FG=![]() ,
,
∴DG=![]() x
x
∴EF=DF=![]() =
=![]()
∵点Q满足∠QDF=∠QED=∠QFE,
∴∠QDF=∠QED=∠QFE,且∠FDE=∠FED,
∴∠QDE=∠QEF,且∠QED=∠QFE,
∴△DQE∽△EQF
∴![]()
∴QE=6,DQ=4
∴DQ+EQ=10
故选:A.

练习册系列答案
相关题目
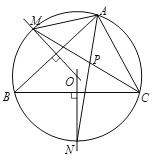
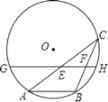
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为8,则GE+FH的最大值为__________ .
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?