Question

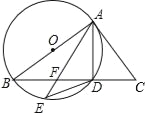
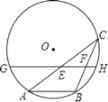
【题目】如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点.若⊙O的半径为8，则GE+FH的最大值为__________ ．

Answer 1

【答案】12

【解析】

由点E、F分别是AC、BC的中点，根据三角形中位线定理得出EF=AB为定值，则GE+FH=GH-EF，所以当GH取最大值时，GE+FH有最大值．而直径是圆中最长的弦，故当GH为⊙O的直径时，即可求得GE+FH的最大值.

解：当GH为⊙O的直径时，GE+FH有最大值，当GH为直径时，E点与O点重合，

∴AC也是直径，AC=16,

∵∠ABC是直径上的圆周角,

∴∠ABC=90°，

∵∠C=30°，

∴AB=AC=8,

∵点E、F分别为AC、BC的中点，

∴EF=AB=4，

∴GE+FH=GH﹣EF=16﹣4=12．

故答案为:12