题目内容
【题目】如图,在![]() 中,
中,
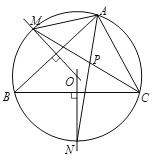
(1)作AB和BC的垂直平分线交于点O;
(2)以点O为圆心,OA长为半径作圆;
(3)⊙O分别与AB和BC的垂直平分线交于点M,N;
(4)连接AM,AN,CM,其中AN与CM交于点P.
根据以上作图过程及所作图形,下列四个结论中,
①![]() ; ②
; ②![]() ;
;
③点O是![]() 的外心 ; ④点P是
的外心 ; ④点P是![]() 的内心.
的内心.
所有正确结论的序号是___________.
【答案】①③④
【解析】
(1)点O是圆心,ON是半径,由垂径定理得 ![]() ,可知
,可知![]()
(2) ![]() 中,AM=BM,AM+BM=2AM>AB,该结论错误.
中,AM=BM,AM+BM=2AM>AB,该结论错误.
(3)三角形三边中垂线的交点是外心,正确.
(4) 由垂径定理知![]() ,所以∠BAN=∠CAN,同理∠BCM=∠ACM,即AN,CM分别为∠BAC和∠ACB的角平分线,因此点P是
,所以∠BAN=∠CAN,同理∠BCM=∠ACM,即AN,CM分别为∠BAC和∠ACB的角平分线,因此点P是![]() 的内心.
的内心.
(1)∵O是![]() 的AB边与BC边的中垂线OM、ON的交点,故点O是外接圆圆心,ON是半径,由垂径定理得
的AB边与BC边的中垂线OM、ON的交点,故点O是外接圆圆心,ON是半径,由垂径定理得 ![]() ,∴
,∴![]()
(2)在 ![]() 中,AM=BM,由三角形两边之和大于第三边可得AM+BM=2AM>AB,该结论错误.
中,AM=BM,由三角形两边之和大于第三边可得AM+BM=2AM>AB,该结论错误.
(3) O是![]() 的AB边与BC边的中垂线OM、ON的交点,故点O是外接圆圆心,正确.
的AB边与BC边的中垂线OM、ON的交点,故点O是外接圆圆心,正确.
(4) 由垂径定理知![]() ,∴∠BAN=∠CAN,同理∠BCM=∠ACM,即AN,CM分别为∠BAC和∠ACB的平分线,因此点P是
,∴∠BAN=∠CAN,同理∠BCM=∠ACM,即AN,CM分别为∠BAC和∠ACB的平分线,因此点P是![]() 的内心.
的内心.

 阅读快车系列答案
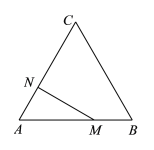
阅读快车系列答案【题目】如图,等边△ABC的边长为3cm,点N在AC边上,AN=1cm.△ABC边上的动点M从点A出发,沿A→B→C运动,到达点C时停止.设点M运动的路程为xcm,MN的长为ycm.
小西根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小西的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
y/cm | 1 | 0.87 | 1 | 1.32 | 2.18 | 2.65 | 2.29 | 1.8 | 1.73 | 1.8 | 2 |
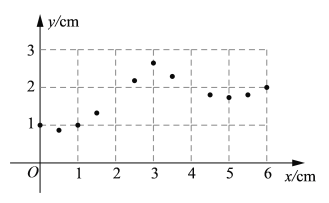
(2)在平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
(3) 结合函数图象,解决问题:当MN=2cm时,点M运动的路程为 cm.
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小娜根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)下表是x与y的几组对应值.
x | … |
|
| 0 |
| 2 |
| 3 | … |
y | … |
|
| 0 | m | n |
| 3 | … |
请直接写出:m= ,n= ;
(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;

(3)结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.