题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,点G是⊙O上一点,AG交CD于点K,延长KD至点E,使KE=GE,分别延长EG、AB相交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC∥EF,试探究KG、KD、GE之间的关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;
(2)连接GD,由平行线的性质得到相等的角,进而根据相似三角形的判定得到△GKD∽△EKG,然后根据相似三角形的对应边成比例可得证;
(3)连接OG,OC,根据平行线的性质得到∠E=∠ACH,然后根据已知的sinE=![]() 设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3
设出AH=3t,则AC=5t,CH=4t,然后根据勾股定理求出CH、AH的长,设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
,由勾股定理得:OH2+CH2=OC2,求出r的值,再由OG的长和tan∠OFG=tan∠CAH,利用三角函数在Rt△OGF中计算出FG的长.
证明:(1)如图1,连接OG.
∵KE=EG,
∴∠EKG=∠EGK,
∵∠AKH=∠EKG,
∴∠EGK=∠AKH,
∴OA=OG,
∴∠OGA=∠OAK,
∵AB⊥CD,
∴∠AHK=90°,
∴∠AKH+∠OAG=90°,
∴∠OGA+∠EGK=90°,
∴∠OGE=90°,
∴EF是⊙O的切线;
(2)KG2=KDGE,理由是:
连接GD,如图2,
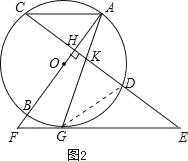
∵AC∥EF,
∴∠C=∠E,
∵∠C=∠AGD,
∴∠E=∠AGD,
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴![]() ,
,
∴KG2=KDEK,
由(1)得:EK=GE,
∴KG2=KDGE;
(3)连接OG,OC,如图3所示,
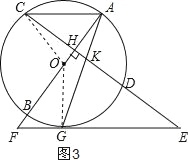
∵AC∥EF,
∴∠E=∠ACH,
∵sinE=sin∠ACH=![]() ,
,
设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=±
)2,解得t=±![]() .
.
∴CH=4![]() ,AH=3
,AH=3![]() ,
,
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3![]() ,
,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3![]() )2+(4
)2+(4![]() )2=r2,解得r=
)2=r2,解得r=![]() ,
,
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() =
=![]() =
=![]() ,
,
∴FG=![]() =
=![]() .
.