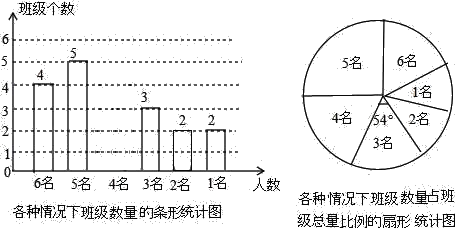
题目内容
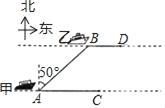
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
【答案】(1)两条航线间的距离为6.43(n mile);(2)还需要0.52h才能使两船的距离最短
【解析】
(1)过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,解直角三角形即可解决问题;
,解直角三角形即可解决问题;
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过![]() 作
作![]() 于
于![]() ,设还需要
,设还需要![]() 小时才能使两船的距离最短,构建方程即可解决问题.
小时才能使两船的距离最短,构建方程即可解决问题.
(1)过点A作AE⊥DB,交DB的延长线于E,
在Rt△AEB中,∵∠AEB=90°,∠EAB=50°,AB=10,
∴AE=ABcos50°=10×0.643=6.43(n mile),
答:两条航线间的距离为6.43(n mile);
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过C作CF⊥BD于F.
∵BE=ABsin50°=7.66,
AC=24×![]() =8,BD=15×
=8,BD=15×![]() =5,
=5,
∴DF=BD+BE﹣AC=4.66,
设还需要t小时才能使两船的距离最短,
则有:24t﹣15t=4.66,
解得t=0.52(h),
答:还需要0.52h才能使两船的距离最短.

练习册系列答案
相关题目