题目内容
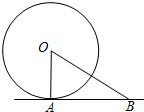
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=
,BC=
,求阴影部分的面积.(计算结果精确到0.1)
(参考数值:π≈3.14,
≈1.41,
≈1.73)

(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=
| ||
| 3 |
4
| ||
| 3 |
(参考数值:π≈3.14,
| 2 |
| 3 |

(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ABD+∠BAD=90°.
又∵∠CBD=∠E,∠BAD=∠E,
∴∠ABD+∠CBD=90°,即∠ABC=90°.
∴BC⊥AB.
∴BC是⊙O的切线.
(2)当点E运动到DE经过点O位置时,△EDB≌△ABD.证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
在△EDB与△ABD中,
,
∴△EDB≌△ABD(AAS).
(3)如图,连接OD,过点O作OF⊥AD于点F,
∵∠BAD=∠E,tanE=
,
∴tan∠BAD=
.
又∵∠ADB=90°,
∴∠BAD=30°.
∵∠ABC=90°,BC=
,
∴AB=
=4.
∴AO=2,OF=1,AF=AOcos∠BAD=
.
∴AD=2
.
∵AO=DO,
∴∠AOD=120°.
∴S阴影=S扇形OAD-S△AOD=
-
×3=2
×1=
π-
≈2.5.

∴∠ADB=90°,
即∠ABD+∠BAD=90°.
又∵∠CBD=∠E,∠BAD=∠E,
∴∠ABD+∠CBD=90°,即∠ABC=90°.
∴BC⊥AB.
∴BC是⊙O的切线.
(2)当点E运动到DE经过点O位置时,△EDB≌△ABD.证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
在△EDB与△ABD中,
|
∴△EDB≌△ABD(AAS).
(3)如图,连接OD,过点O作OF⊥AD于点F,
∵∠BAD=∠E,tanE=
| ||
| 3 |
∴tan∠BAD=
| ||
| 3 |
又∵∠ADB=90°,
∴∠BAD=30°.
∵∠ABC=90°,BC=
4
| ||
| 3 |
∴AB=
| BC |
| tan∠DAB |
∴AO=2,OF=1,AF=AOcos∠BAD=
| 3 |
∴AD=2
| 3 |
∵AO=DO,
∴∠AOD=120°.
∴S阴影=S扇形OAD-S△AOD=
| 120π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 半径为r.
半径为r.