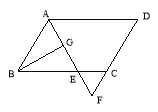
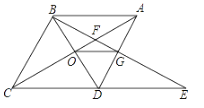
题目内容
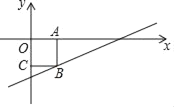
【题目】如图所示,观察数轴,请回答:
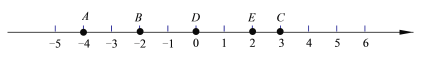
(1)点C与点D的距离为______ ,点B与点D的距离为______ ;
(2)点B与点E的距离为______ ,点A与点C的距离为______ ;
发现:在数轴上,如果点M与点N分别表示数m,n,则他们之间的距离可表示为 ______(用m,n表示)
(3)利用发现的结论解决下列问题: 数轴上表示x的点P与B之间的距离是1,则 x 的值是______ .
【答案】(1)3 , 2 ;
(2)4,7,![]() ;
;
(3)-1或-3.
【解析】
(1)直接根据数轴上两点间距离的定义解答即可;
(2)根据数轴上两点间距离的定义进行解答,再进行总结规律,即可得出MN之间的距离;
(3)根据(2)得出的规律,进行计算即可得出答案.
解:(1)由图可知,点C与点D的距离为3,点B与点D的距离为2.
故答案为:3,2;
(2)由图可知,点B与点E的距离为4,点A与点C的距离为7;
如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为MN=|m-n|.
故答案为:4,7,|m-n|;
(3)由(2)可知,数轴上表示x的点P与表示-2的点B之间的距离是1,则|x+2|=1,解得x=-1或x=-3.
故答案为:-1或-3.

【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
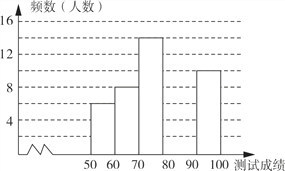
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?