题目内容
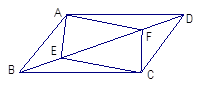
已知：如图，四边形ABCD中，E、F、G、H分别是AB、 BC、CD、DA的中点。求证：四边形EFGH是平行四边形(本题6分)
连接AC
∵△ACD, G、H分别是CD、DA的中点
∴HG∥AC, HG=
AC
同理，EF∥AC, EF=AC
∴HG∥EF, HG=EF
∴四边形EFGH是平行四边形
∵△ACD, G、H分别是CD、DA的中点
∴HG∥AC, HG=
AC同理，EF∥AC, EF=
AC∴HG∥EF, HG=EF
∴四边形EFGH是平行四边形
做出辅助线，连接AC，根据G、H分别是边AB、BC的中点，得到GH平行且等于AC的一半，又E、F分别是边CD、DA的中点，得到MN平行且等于AC的一半，这样一对对边平行且相等，得到四边形是一个平行四边形．
练习册系列答案
相关题目
,则
等于( ) 
为何值时，四边形
的面积是梯形
的面积的一半；
，BE=2
