题目内容
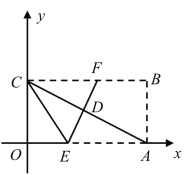
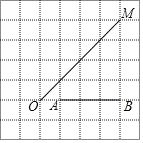
【题目】如图,在每个小正方形的边长为1的网格中,点O,A,B,M均在格点上,P为线段OM上的一个动点.
(1)OM的长等于_______;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的.
【答案】(1)4![]() ;(2)见解析;
;(2)见解析;
【解析】
解:(1)由勾股定理可得OM的长度
(2)取格点 F , E, 连接 EF , 得到点 N ,取格点S, T, 连接ST, 得到点R, 连接NR交OM于P,则点P即为所求。
(1)OM=![]() =4
=4![]() ;
;
故答案为4![]() .
.
(2)以点O为原点建立直角坐标系,则A(1,0),B(4,0),设P(a,a),(0≤a≤4),
∵PA2=(a﹣1)2+a2,PB2=(a﹣4)2+a2,
∴PA2+PB2=4(a﹣![]() )2+
)2+![]() ,
,
∵0≤a≤4,
∴当a=![]() 时,PA2+PB2 取得最小值
时,PA2+PB2 取得最小值![]() ,
,
综上,需作出点P满足线段OP的长=![]() ;
;
取格点F,E,连接EF,得到点N,取格点S,T,连接ST,得到点R,连接NR交OM于P,
则点P即为所求.

练习册系列答案
相关题目