题目内容
【题目】已知，如图，
和
都是等边三角形，且点
在
上．
（1）求证：
（2）直接写出
和
之间的关系；
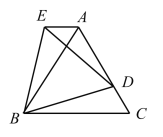
【答案】（1）证明见解析；（2）AE+AD=AB
【解析】
（1）利用等边三角形的性质，证明△DBC≌△EBA，得到∠EAB=∠ABC，即可判断；
（2）利用（1）中全等三角形的性质得出CD=AE，即可得到AE、AD、AB的关系.
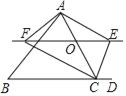
解：（1）证明：∵△ABC和△BDE都是等边三角形，
∴AB=BC，BE=BD，∠ABC=∠DBE=∠C=60°
∴∠ABC-∠ABD=∠DBE-∠ABD
∴∠DBC=∠EBA
∴△DBC≌△EBA（SAS）
∴∠C=∠EAB=∠ABC
∴EA∥BC
（2）∵△DBC≌△EBA
∴CD=AE，
∵CD+AD=AC=AB，
∴AE+AD=AB.
新思维假期作业寒假吉林大学出版社系列答案
【题目】某共享单车公司提供了手机和会员卡两种支付方式．若用手机支付方式，骑行时间在半小时以内（含半小时）不收费，超出半小时后每半小时收费1元，若选择会员卡支付，骑行时间每半小时收费0.8元，设骑行时间为x小时．
（1）根据题意，填写下表（单位：元）：
骑行时间（小时） | 0.5 | 2 | 3 | … |
手机支付付款金额（元） | 0 | … | ||
会员卡支付付款金额（元） | 3.2 | … |
（2）设用手机支付付款金额为y1元，用会员卡支付付款金额为y2元，分别写出y1，y2关于x的函数关系式；
（3）若李老师经常骑行该公司的共享单车，他应选择哪种支付方式比较合算？
【题目】某公司为一种新型电子产品在该城市的特约经销商，已知每件产品的进价为40元，该公司每年销售这种产品的其他开支（不含进货价）总计100万元，在销售过程中得知，年销售量y（万件）与销售单价x（元）之间存在如表所示的函数关系，并且发现y是x的一次函数．
销售单价x（元） | 50 | 60 | 70 | 80 |
销售数量y（万件） | 5.5 | 5 | 4.5 | 4 |
（1）求y与x的函数关系式；
（2）问：当销售单价x为何值时，该公司年利润最大？并求出这个最大值；
【备注：年利润=年销售额﹣总进货价﹣其他开支】
（3）若公司希望年利润不低于60万元，请你帮助该公司确定销售单价的范围．
