题目内容
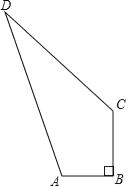
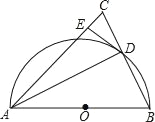
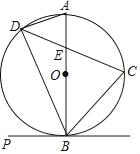
【题目】如图,C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CEDE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)由AB是⊙O的直径知∠BAD+∠ABD=90°,由PB是⊙O的切线知∠PBD+∠ABD=90°,据此可得答案;
(2)连接OC,设圆的半径为r,则OA=OB=OC=r,证△ADE∽△CBE得DECE=AEBE=r2-OE2,由![]() 知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
(3)先求出BC=4![]() 、CE=2
、CE=2![]() ,根据BC2-CE2=CEDE计算可得.
,根据BC2-CE2=CEDE计算可得.
(1)∵AB是⊙O的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB是⊙O的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴![]() ,即DECE=AEBE,
,即DECE=AEBE,
如图,连接OC,

设圆的半径为r,则OA=OB=OC=r,
则DECE=AEBE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵![]() ,
,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DECE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC=![]() =4
=4![]() ,
,
又∵E是半径OA的中点,
∴AE=OE=2,
则CE=![]() =
=![]() =2
=2![]() ,
,
∵BC2﹣CE2=DECE,
∴(4![]() )2﹣(2
)2﹣(2![]() )2=DE2
)2=DE2![]() ,
,
解得:DE=![]() .
.

练习册系列答案
相关题目