题目内容
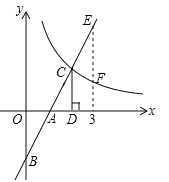
【题目】已知抛物线y=ax2+bx+c经过点A(-1,0),且经过直线y=x-2与x轴的交点B及与y轴的交点C.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标;
(3)若点M在第四象限内的抛物线上,且tan∠MOC=1,求M点的坐标及四边形OBMC面积.
【答案】(1)y=x2-x-2;(2)顶点坐标为(![]() ,-
,-![]() );(3)M(
);(3)M(![]() ,-
,-![]() ),四边形OBMC的面积为2
),四边形OBMC的面积为2![]() .
.
【解析】
(1)先根据坐标轴上点的坐标特征确定B(2,0),C(0,2),然后利用待定系数法确定二次函数解析式;
(2)把(1)的解析式![]() 配成顶点式得y=
配成顶点式得y=![]() ,然后根据二次函数的性质确定顶点坐标;
,然后根据二次函数的性质确定顶点坐标;
(3)由于△OBC为等腰直角三角形,而OM⊥BC,则OM的解析式为![]() ,可设
,可设![]() ,把它代入二次函数解析式得
,把它代入二次函数解析式得![]() ,解得
,解得![]() .则M点坐标为
.则M点坐标为![]() ,然后计算出OM=2,BC=
,然后计算出OM=2,BC=![]() ,再利用三角形面积公式计算四边形OBMC的面积.
,再利用三角形面积公式计算四边形OBMC的面积.
解:(1)直线y=x-2与坐标轴的交点坐标分别为B(2,0),C(0,-2),以A、B、C三点的坐标分别代入抛物线y=ax2+bx+c中,得
解得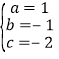
∴所求抛物线的解析式是y=x2-x-2;
(2)∵y=x2-x-2=![]() ,
,
∴抛物线的顶点坐标为(![]() ,-
,-![]() );
);
(3)∵点M在第四象限内的抛物线上,且tan∠MOC=1,
∴设M(x,-x),
因为点M在抛物线上,∴x2-x-2=-x.
解得x1=![]() ,x2=
,x2=![]() ,
,
因点M在第四象限,取![]() ,∴M(
,∴M(![]() ,-
,-![]() ),
),
∵OB=OC,∠BOC=90°,
∴∠OCB=45°,
∵∠COM=45°,
∴∠ODC=90°,
即OM⊥BC,
得OM=2,BC=2![]() ,
,
∴四边形OBMC的面积为![]() OMBC=2
OMBC=2![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目