题目内容
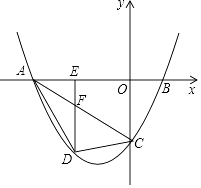
【题目】已知：如图，直线y=﹣ 
x﹣3与坐标轴交于点A，C，经过点A，C的抛物线y=ax2+bx﹣3与x轴交于点B（2，0）．
（1）求抛物线的解析式；
（2）点D是抛物线在第三象限图象上的动点，是否存在点D，使得△DAC的面积最大？若存在，请求这个最大值并求出点D的坐标；若不存在，请说明理由；
（3）过点D作DE⊥x轴于E，交AC于F，若AC恰好将△ADE的面积分成1：4两部分，请求出此时点D的坐标．
【答案】
（1）
解：（1）在y=﹣ 
x﹣3中，当y=0时，x=﹣6，
即点A的坐标为：（﹣6，0），
将A（﹣6，0），B（2，0）代入y=ax2+bx﹣3得：
，
解得： 
，
∴抛物线的解析式为：y= 
x2+x﹣3；
（2）
解：设点D的坐标为：（m， m2+m﹣3），则点F的坐标为：（m，﹣ m﹣3），
∴DF=﹣ m﹣3﹣（ m2+m﹣3）=﹣ m2﹣ 
m，
∴S△ADC=S△ADF+S△DFC
= DFAE+ DFOE
= DFOA
= ×（﹣ m2﹣ m）×6
=﹣ 
m2﹣ 
m
=﹣ （m﹣3）2+ 
，
∵a=﹣ ＜0，
∴抛物线开口向下，
∴当m=3时，S△ADC存在最大值 ，
又∵当m=3时， m2+m﹣3=﹣ 
，
∴存在点D（3，﹣ ），使得△ADC的面积最大，最大值为 ；
（3）
解：由题意可得△ADE的面积分成1：4两部分即是点F将DE分成1：4两部分
①当DF：EF=1：4时，（﹣ m2﹣ m）：（ m+3）=1：4，
解得：m1=﹣ ，m2=﹣6（不合题意，舍去），
当m=﹣ 时， m2+m﹣3=﹣ 
，
∴点D的坐标为：（﹣ ，﹣ ），
②当DF：EF=4：1时，（﹣ m2﹣ m）：（ m+3）=4：1，
解得：m1=﹣6（不合题意，舍去），m2=﹣8（不合题意，舍去），
综上所述存在点D（﹣ ，﹣ ），使得AC恰好将△ADE的面积分成1：4两部分．
【解析】解：（1）在y=﹣ x﹣3中，当y=0时，x=﹣6，即点A的坐标为：（﹣6，0），将A（﹣6，0），B（2，0）代入y=ax2+bx﹣3得： ，
解得： ，∴抛物线的解析式为：y= x2+x﹣3；（2）设点D的坐标为：（m， m2+m﹣3），则点F的坐标为：（m，﹣ m﹣3），∴DF=﹣ m﹣3﹣（ m2+m﹣3）=﹣ m2﹣ m，∴S△ADC=S△ADF+S△DFC= DFAE+ DFOE= DFOA= ×（﹣ m2﹣ m）×6=﹣ m2﹣ m=﹣ （m﹣3）2+ ，∵a=﹣ ＜0，∴抛物线开口向下，∴当m=3时，S△ADC存在最大值 ，又∵当m=3时， m2+m﹣3=﹣ ，∴存在点D（3，﹣ ），使得△ADC的面积最大，最大值为 ；（3）由题意可得△ADE的面积分成1：4两部分即是点F将DE分成1：4两部分①当DF：EF=1：4时，（﹣ m2﹣ m）：（ m+3）=1：4，解得：m1=﹣ ，m2=﹣6（不合题意，舍去），当m=﹣ 时， m2+m﹣3=﹣ ，∴点D的坐标为：（﹣ ，﹣ ），②当DF：EF=4：1时，（﹣ m2﹣ m）：（ m+3）=4：1，解得：m1=﹣6（不合题意，舍去），m2=﹣8（不合题意，舍去），综上所述存在点D（﹣ ，﹣ ），使得AC恰好将△ADE的面积分成1：4两部分．
【考点精析】利用二次函数的最值对题目进行判断即可得到答案，需要熟知如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．
