题目内容
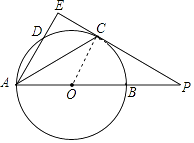
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且 ![]() =
= ![]() ,弦AD的延长线交切线PC于点E,连接AC.
,弦AD的延长线交切线PC于点E,连接AC. 
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP= ![]() ,求AE的长.
,求AE的长.
【答案】
(1)解:连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵BC=CD,
∴∠OAC=∠CAD.
∴∠OCA=∠CAD,
∴OC∥AE.
∴∠E=∠OCP.
∵PE是的切线,C为切点,
∴∠OCP=90°.
∴∠E=90°
(2)解:在Rt△ABD中,OC=2.5,sin∠P= ![]() =
= ![]() ,
,
∴OP= ![]() ,
,
在Rt△APE中,AP= ![]() +2.5=
+2.5= ![]() ,sin∠P=
,sin∠P= ![]() =
= ![]() ,
,
∴AE=4.
【解析】(1)连接OC.根据等腰三角形的性质得到∠OAC=∠OCA.∠OAC=∠CAD.推出OC∥AE.根据平行线的性质得到∠E=∠OCP.根据切线的性质即可得到结论;(2)解直角三角形即可得到结论.
【考点精析】利用切线的性质定理和解直角三角形对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目