题目内容
【题目】如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.

【答案】![]()
【解析】试题分析:设AC、AB与⊙O的切点分别为R、M,连接OR、OM,过O作OK⊥BC于K;由于△POR∽△PCB,可得出关于PR,OR,PC,BC的比例关系式,由此可求出PR与半径的比例关系.由此可表示出OK,AP的长;在Rt△OBK中,已知了OK的表达式,BK=BC-r,而OB可在Rt△OBM中用勾股定理求得.由此可根据勾股定理求出半径r的长.
试题解析:
连接OR、OM,如图所示:
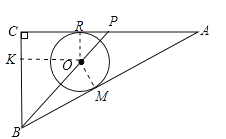
则OR⊥AC,OM⊥AB;过O作OK⊥BC于K,
设⊙O的半径为r,
易知:△POR∽△PBC,
![]() ,
,
∵BC=![]() cm,
cm,
∴![]() ,即PR=
,即PR=![]() ,
,
AP=CP=2×2=4cm,
在Rt△BOK与Rt△BMO中,根据勾股定理,得:
![]() ,
,
解得:r=![]() cm.
cm.

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入/元 | |
A种型号/台 | B种型号/台 | ||
第1周 | 3 | 5 | 1800 |
第2周 | 4 | 10 | 3200 |
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?






