题目内容
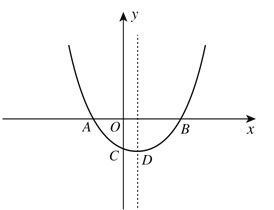
【题目】如图,抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3) 点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似,若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ,D(
,D(![]() ,
,![]() );(2)P(
);(2)P(![]() ,
,![]() );(3)存在.N(
);(3)存在.N(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可;
(3)作出辅助线,利用tan∠MDN=2或![]() ,建立关于点N的横坐标的方程,求出即可.
,建立关于点N的横坐标的方程,求出即可.
试题解析:(1)由于抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入
(a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入![]() (a≠0),可得:
(a≠0),可得:![]() ;解方程组可得:
;解方程组可得: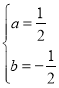 ,故抛物线的解析式为:
,故抛物线的解析式为:![]() ,∵
,∵![]() =
=![]() ,所以D的坐标为(
,所以D的坐标为(![]() ,
,![]() ).
).
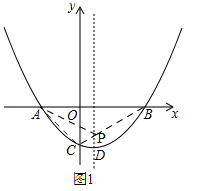
(2)如图1,设P(![]() ,k),∵
,k),∵![]() ,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:
,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:![]() ,解得:
,解得: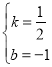 ,∴直线BC为:
,∴直线BC为:![]() .当x=
.当x=![]() 时,
时,![]() =
=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
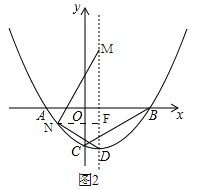
(3)存在.如图2,过点作NF⊥DM,∵B(2,0),C(0,﹣1),∴OB=2,OC=1,∴tan∠OBC=![]() ,tan∠OCB=
,tan∠OCB=![]() =2,设点N(m,
=2,设点N(m,![]() ),∴FN=|m﹣
),∴FN=|m﹣![]() |,FD=|
|,FD=|![]() |=|
|=|![]() |,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
|,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
①当∠MDN=∠OBC时,∴tan∠MDN=![]() =
=![]() ,∴
,∴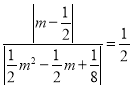 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②当∠MDN=∠OCB时,∴tan∠MDN=![]() =2,∴
=2,∴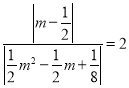 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
∴符合条件的点N的坐标(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).