题目内容
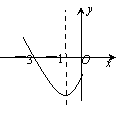
【题目】如图(1),直线![]() 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8![]() ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
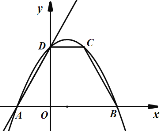
图(1)
(1) 求抛物线的解析式;
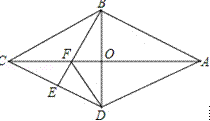
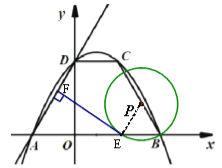
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与![]() 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
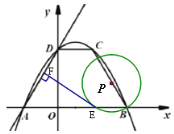
图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)EF与⊙P相切.,证明见解析;(3) 存在, x=
;(2)EF与⊙P相切.,证明见解析;(3) 存在, x=![]() ,P(
,P(![]() ,
,![]() ).
).
【解析】
试题(1)过C作CE⊥AB于E,利用矩形的性质分别求得三点的坐标,利用求得的点的坐标,用待定系数法求得二次函数的解析式即可;
(2)连结PE,可以得到:PE∥DA,从而得出EF与⊙P相切;
(3)设⊙P与y轴相切于点G,P作PQ⊥x轴于点Q,设Q(x,0),用含有x的代数式分别表示出PG和PB,再根据PG=PB求出x的值即可.
试题解析:(1) ∵![]() ,当x=0时, y=
,当x=0时, y=![]() ;当y=0时,x=-2,
;当y=0时,x=-2,
∴A(-2,0),D![]() ,
,
∵ABCD为等腰梯形,
∴AD=BC,∠OAD=∠OBC
过点C作CH⊥AB于点H,则AO=BH,OH=DC.
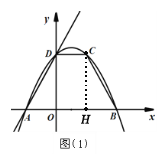
∵ABCD的面积是![]() ,
,
∴8![]() =
=![]() ,
,
∴DC=2,
∴C(2, ![]() ),B(4,0),
),B(4,0),
设抛物线解析式为![]() (
(![]() ),代入A(-2,0),D
),代入A(-2,0),D![]() ,B(4,0)
,B(4,0)
得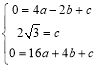 ,
,
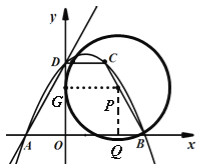
解得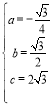 ,
,
即![]() ;
;
(2)连结PE,∵PE=PB,
∴∠PBE=∠PEB,
∵∠PBE=∠DAB,
∴∠DAB=∠PBE,
∴PE∥DA,
∵EF⊥AD,
∴∠FEP=∠AFF=90°,
又PE为半径,EF与⊙P相切.;
(3)设⊙P与y轴相切于点G,P作PQ⊥x轴于点Q,
设Q(x,0),则QB=4-x,
∵∠PBA=∠DAO,![]() ,
,
∴∠PBA=∠DAO=60°,
∴PQ=![]() , PB=8-2x ,P(x,
, PB=8-2x ,P(x, ![]() ),
),
∵⊙P与y轴相切于点G,⊙P过点B,
∴PG=PB,
∴x=8-2x,
∴x=![]() ,P(
,P(![]() ,
,![]() ).
).

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案