题目内容
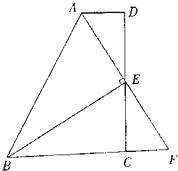
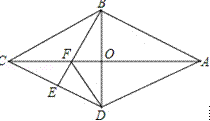
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
【答案】(1)证明见解析;(2)四边形ABCD的周长为8.
【解析】试题分析:(1)首先利用SSS定理证明△ABC≌△ADC可得∠BCA=∠DCA即可证明△CBF≌△CDF.
(2) 由△CBF≌△CDF,可知,∠BCF=∠DCF,又CB=CD,得出OB=OD,∠COB=∠COD=90°,因为OC=OA,所以AC与BD互相垂直平分,即可证得四边形ABCD是菱形,然后根据勾股定理全等AB长,进而求得四边形的面积.
试题解析(1)证明:在△ABC和△ADC中, 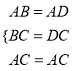 ,
,
∴△ABC≌△ADC(SSS),
∴∠BCA=∠DCA,
在△CBF和△ADF中, 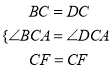 ,
,
∴△CBF≌△CDF(SAS)
(2)∵△CBF≌△CDF,
∴∠BCF=∠DCF,
∴OB=OD,BD⊥AC,
∵OA=OC,
∴四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AC=2![]() ,BD=2,
,BD=2,
∴OA=![]() ,OB=1,
,OB=1,
∴AB=![]() ,
,
∴四边形ABCD的周长=4AB=4×2=8.

练习册系列答案
相关题目