题目内容
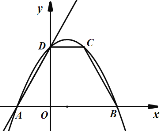
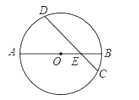
【题目】如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2![]() ,则∠AED的度数是( )
,则∠AED的度数是( )
A. 30° B. 60° C. 45° D. 36°
【答案】C
【解析】
连接OD,过圆心O作OH⊥CD于点H.根据垂径定理求得DH=CH=![]() CD=
CD=![]() ;然后根据已知条件“AE=6,BE=2”求得⊙O的直径,从而知⊙O的半径;最后利用勾股定理求得OH=1,再边角关系得到∠AED=45°.
;然后根据已知条件“AE=6,BE=2”求得⊙O的直径,从而知⊙O的半径;最后利用勾股定理求得OH=1,再边角关系得到∠AED=45°.
解:连接OD,过圆心O作OH⊥CD于点H.
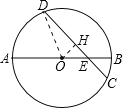
∴DH=CH=![]() CD(垂径定理);
CD(垂径定理);
∵CD=2![]() ,
,
∴DH=![]() .
.
又∵AE=6,BE=2,
∴AB=8,
∴OA=OD=4(⊙O的半径);
∴OE=2;
∴在Rt△ODH中,OH=![]() =
=![]() =
=![]() (勾股定理);
(勾股定理);
在Rt△OEH中,sin∠OEH=![]() =
=![]() ,
,
∴∠OEH=45°,
即∠AED=45°.
故选:C.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
【题目】王老师将1个黑球和若干个白球(这些球除颜色外都相同)放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出1个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸出黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)根据上表数据估计从袋中摸出1个球是黑球的概率是_________;
(2)估计袋中白球的个数.