题目内容
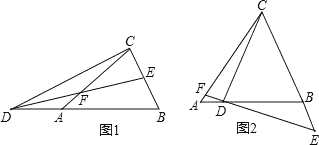
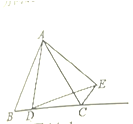
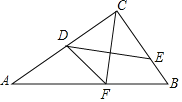
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别在AC、BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处,若AC=12,AB=13,则CD的长为_________.
【答案】![]() .
.
【解析】
由对称性可知CF⊥DE,可得∠CDE=∠ECF=∠B,得出CF=BF,同理可得CF=AF,由此可得F是AB的中点,求得CF=5,再判定△CDF∽△CFA,得到CF2=CD×CA,进而得出CD的长.
由对称性可知CF⊥DE,
又∵∠DCE=90°,
∴∠CDE=∠ECF=∠B,
∴CF=BF,
同理可得CF=AF,
∴F是AB的中点,
∴CF=![]() AB=
AB=![]() ,
,
又∵∠DFC=∠ACF=∠A,∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即(![]() )2=CD×12,
)2=CD×12,
∴CD=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目