Question

【题目】如图，△ABC和△ACD都是边长为2厘米的等边三角形，两个动点P，Q同时从A点出发，点P以0.5厘米/秒的速度沿A→C→B的方向运动，点Q以1厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动。设P、Q运动的时间为t秒

(1)当t=2时，PQ=___；

(2)求点P、Q从出发到相遇所用的时间；

(3)当t取何值时，△APQ是等边三角形；请说明理由.

Answer 1

【答案】（1）；（2）t=4；（3）t=.

【解析】

(1)、先求出AP，AQ的长度，再根据等边三角形的性质得到△APQ为直角三角形，利用勾股定理即可解答；(2)、△ABC是等边三角形，边长是2厘米．点P、Q从出发到相遇，即两人所走的路程的和是6cm．设从出发到相遇所用的时间是t秒．列方程就可以求出时间；(3)、当P在AC上，Q在AB上时，AP≠AQ，则一定不是等边三角形，当△APQ是等边三角形时，Q一定在边CD上，P一定在边CB上，若△APQ是等边三角形，则CP=DQ，根据这个相等关系，就可以得到一个关于t的方程，就可以得到t的值．

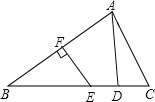
(1)、当t=2时，AP=2×0.5=1厘米，AQ=2×1=2厘米，

如图1，

∵△ABC是边长为2厘米的等边三角形，∴PQ⊥AC，∴PQ=；

(2)、由0.5t+t=6， 解得t=4.

(3)、当0t4时，都不存在；

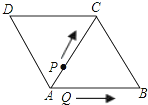
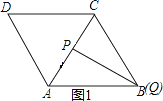
当4<t6时，如图2，若△APQ是等边三角形，

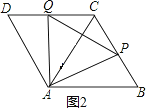
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP，则CP=DQ，即6t=0.5t2，解得：t=.