Question

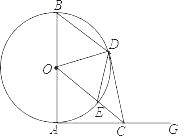
【题目】如图，直线y＝﹣x+5与x轴交于点B，与y轴交于点C，抛物线y＝﹣x2+bx+c与直线y＝﹣x+5交于B，C两点，已知点D的坐标为（0，3）

（1）求抛物线的解析式；

（2）点M，N分别是直线BC和x轴上的动点，则当△DMN的周长最小时，求点M，N的坐标，并写出△DMN周长的最小值；

（3）点P是抛物线上一动点，在（2）的条件下，是否存在这样的点P，使∠PBA＝∠ODN？若存在，请直接写出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x2+4x+5；（2）点M、N的坐标分别为（，）、（，0），△DMN周长的最小值＝；（3）点P（﹣，）．

【解析】

（1）求出点B、C的坐标、将点B、C坐标代入二次函数表达式，即可求解；

（2）过点D分别作x轴和直线BC的对称点D′（0，-3）、D″，连接D′D″交x轴、直线BC于点N、M，此时△DMN的周长最小，即可求解；

（3）tan∠ODN==tan∠PBA，确定直线BP的表达式，即可求解．

（1）y＝﹣x+5，令x＝0，则y＝5，令y＝0，则x＝5，

故点B、C的坐标分别为（5，0）、（0，5），

则二次函数表达式为：y＝﹣x2+bx+5，将点B坐标代入上式并解得：b＝4，

故抛物线的表达式为：y＝﹣x2+4x+5…①，

令y＝0，则x＝﹣1或5，

故点A（﹣1，0），而OB＝OC＝2，故∠OCB＝45°；

（2）过点D分别作x轴和直线BC的对称点D′（0，﹣3）、D″，

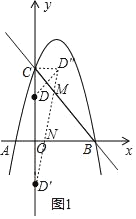
∵∠OCB＝45°，则CD″∥x轴，则点D″（2，5），

连接D′D″交x轴、直线BC于点N、M，此时△DMN的周长最小，

将点D′、D″的坐标代入一次函数表达式：y＝mx+n并解得：

直线D′D″的坐标代入一次函数表达式为：y＝4x﹣3，

则点M、N的坐标分别为（，）、（，0），

△DMN周长的最小值＝DM+DN+MN＝；

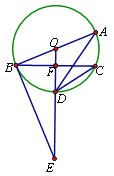
（3）如图2，tan∠ODN＝＝tan∠PBA，

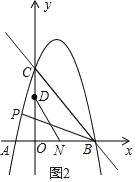
则直线BP的表达式为：y＝﹣x+s，将点B的坐标代入上式并解得：

直线BP的表达式为：y＝﹣x+…②，

联立①②并解得：x＝5或﹣（舍去5）

故：点P（﹣，）．