Question

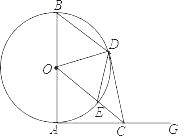
【题目】如图，AB为⊙O的直径，射线AG为⊙O的切线，点A为切点，点C为射线AG上任意一点，连接OC交⊙O于点E，过点B作BD∥OC交⊙O于点D，连接CD，DE，OD．

（1）求证：△OAC≌△ODC；

（2）①当∠OCA的度数为　 　时，四边形BOED为菱形；

②当∠OCA的度数为　 　时，四边形OACD为正方形．

Answer 1

【答案】（1）证明见解析；（2）①∠OCA＝30°，②∠OCA＝45°．

【解析】

（1）依据SAS可证明△OAC≌△ODC；

（2）①依据菱形的四条边都相等，可得△OBD是等边三角形，则∠AOC=∠OBD=60°，求出∠OCA=30°；②由正方形的性质得出∠ACD=90°，则∠ACO=45°．

（1）证明：∵OB＝OD，

∴∠B＝∠ODB，

∵BD∥OC，

∴∠AOC＝∠B，∠DOC＝∠ODB，

∴∠AOC＝∠COD，

∵OA＝OD，OC＝OC，

∴△OAC≌△ODC（SAS）；

（2）①∵四边形BOED是菱形，

∴OB＝DB．

又∵OD＝OB，

∴OD＝OB＝DB．

∴△OBD为等边三角形，

∴∠OBD＝60°．

∵CO∥DB，

∴∠AOC＝60°，

∵射线AG为⊙O的切线，

∴OA⊥AC，

∴∠OAC＝90°，

∴∠OCA＝∠OAC﹣∠AOC＝90°﹣60°＝30°，

②∵四边形OADC是正方形，

∴∠ACD＝90°，

∵∠ACO＝∠DCO，

∴∠OCA＝45°，

故答案为：30°，45°．