Question

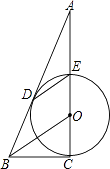
【题目】如图，△ABC是等边三角形，D、E在BC边所在的直线上，且BC2=BDCE．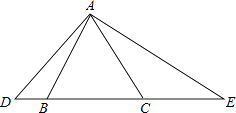

（1）求∠DAE的度数．
（2）求证：AD2=DBDE．

Answer 1

【答案】
（1）解：∵△ABC是等边三角形，

∴∠ABC=∠ACB=60°，AB=AC=BC，

∴∠ABD=∠ACE，

∵BC2=BDCE，

∴ABAC=BDCE，

即 ，

∴△ABD∽△ECA；

∴∠DAB=∠E，

∴∠DAE=∠DAB+∠BAC+∠EAC=120°

（2）证明：∵∠DAE=∠ADB=120°，∠D=∠D，

∴△ABD∽△EAD

∴ ，

∴AD2=DBDE

【解析】（1）根据等边三角形的性质得到∠ABC=∠ACB=60°，利用等角的补角相等得到∠ABD=∠ACE，然后把题中已知的等式化为比例的形式，根据两边对应成比例，且夹角对应相等的两三角形相似即可得证；（2）由于∠DAE=∠ADB=120°，∠D=∠D，推出△ABD∽△EAD根据相似三角形的性质得到 ，即可得到结论．