题目内容
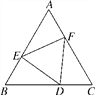
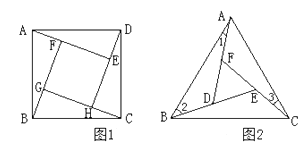
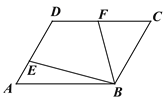
【题目】如图,□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°,若AE=2,FC=3,则EF的长度为_________________.
【答案】![]()
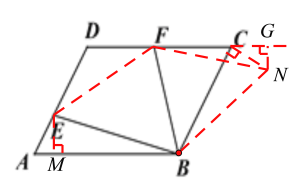
【解析】由DE=DF,AE=2,FC=3可知AB-BC=1,过点E作EM⊥AB垂足为M,根据30度角所对的直角边等于斜边的一半可得AM=1,进而得出BM=BC,将△BEM顺时针旋转120°得△BEN,连接FN,可证△BFE≌△BFN,即可得出EF=FN,过点N作NG⊥DC交DC的延长线于点G,利用勾股定理即可求出答案.
过点E作EM⊥AB垂足为M,
在Rt△AEM中,
∵∠A=60°,
∴∠AEM=30°,
∴AM=![]() AE=1,
AE=1,
∴ME=![]() ,
,
∵DE=DF,AE=2,FC=3
∴DC-AD=1,
即AB-BC=1,
∴BM=BC,
将△BEM顺时针旋转120°得△BEN,连接FN,则CN=EM=![]() ,BE=BN,
,BE=BN,
∵∠EBF=60°,∠EBN=120°,
∴∠NBF=60°,
∴∠EBF=∠NBF,
∵BE=BN,BF=BF,
∴△BFE≌△BFN,
∴EF=FN,
过点N作NG⊥DC交DC的延长线于点G,
∵∠GCN=180°-60°-90°=30°,
∴NG=![]() NC=
NC=![]() ,
,
∴CG=![]() =
=![]() ,
,
∴FG=3+![]() =
=![]() ,
,
∴FN=![]() =
=![]() ,
,
∴EF=![]() .
.
故答案为:![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目