题目内容
△ABC中，∠C=90°，AD为角平分线，BC=32，BD：DC=9：7，则点D到AB的距离为
- A.18cm
- B.16cm
- C.14cm
- D.12cm
C
分析：根据题意画出图形分析．根据已知线段长度和关系可求DC的长；根据角平分线性质解答．
解答：
解：如图所示．
作DE⊥AB于E点．
∵BC=32，BD：DC=9：7，
∴CD=32×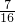
=14．
∵AD平分∠CAB，∠C=90°，DE⊥DE，
∴DE=DC=14．
即D点到AB的距离是14cm．
故选C．
点评：此题考查角平分线的性质，属基础题．
分析：根据题意画出图形分析．根据已知线段长度和关系可求DC的长；根据角平分线性质解答．
解答：
解：如图所示．作DE⊥AB于E点．
∵BC=32，BD：DC=9：7，
∴CD=32×
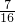=14．∵AD平分∠CAB，∠C=90°，DE⊥DE，
∴DE=DC=14．
即D点到AB的距离是14cm．
故选C．
点评：此题考查角平分线的性质，属基础题．
练习册系列答案
相关题目
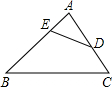如图，在△ABC中，AC=2，AB=3，D是AC上一点，E是AB上一点，且∠ADE=∠B，设AD=x，AE=y，则y与x之间的函数关系式是（ ）A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
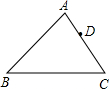如图，在△ABC中，AB=8，AC=6，BC=7，点D在AC上，AD=2，