题目内容
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
【答案】(1)见解析;(2)t的值为2-2![]() ≤t≤2+2
≤t≤2+2![]() ;(3)k的值为-3+
;(3)k的值为-3+![]() 或1-
或1-![]() .
.
【解析】
(1)如图1中,作OH⊥AB于H.求出OH即可解决问题.
(2)如图2中,作TH⊥AB于H,交⊙T于D.分两种情形求出d(⊙T,直线AB)=1时,点T的坐标即可.
(3)当直线经过点D(2-![]() ,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-
,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-![]() ,求出直线y=kx经过点E,点F时,k的值即可.
,求出直线y=kx经过点E,点F时,k的值即可.
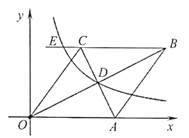
(1)如图1中,作OH⊥AB于H.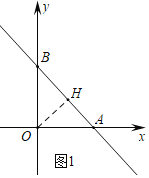
∵A(2,0),B(0,2),
∴OA=OB=2,AB=2![]() ,
,
∵![]() ×OA×OB=
×OA×OB=![]() ×AB×OH,
×AB×OH,
∴OH=![]() ,
,
∴d(点O,直线AB);
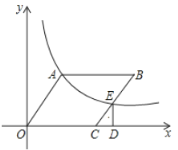
(2)如图2中,作TH⊥AB于H,交⊙T于D.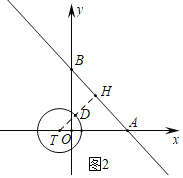
当d(⊙T,直线AB)=1时,DH=1,
∴TH=2,AT=2![]() ,
,
∴OT=2![]() -2,
-2,
∴T(2-2![]() ,0),
,0),
根据对称性可知,当⊙T在直线AB的右边,满足d(⊙T,直线AB)=1时,T(2+2![]() ,0),
,0),
∴满足条件的t的值为2-2![]() ≤t≤2+2
≤t≤2+2![]() .
.
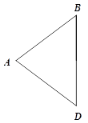
(3)如图3中,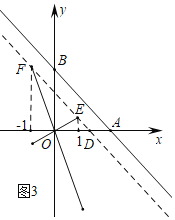
当直线经过点D(2-![]() ,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-
,0)与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为y=-x+2-![]() ,
,
当直线y=kx经过E(1,1-![]() )时,k=1-
)时,k=1-![]() ,
,
当直线y=kx经过F(-1,3-![]() ),k=-3+
),k=-3+![]() ,
,
综上所述,满足条件的k的值为-3+![]() 或1-
或1-![]() .
.