题目内容
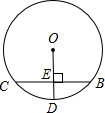
如图所示，某窗户由矩形和弓形组成，已知弓形的跨度AB=3m，弓形的高EF=1m，现计划安装玻璃，请帮工程师求出
所在圆O的半径r．
 |
| AB |
∵弓形的跨度AB=3m，EF为弓形的高，
∴OE⊥AB，
∴AF=
AB=
m，
∵
所在圆O的半径为r，弓形的高EF=1m，
∴AO=r，OF=r-1，
在Rt△AOF中，AO2=AF2+OF2，
即r2=（
）2+（r-1）2，
解得r=
（m）．
答：
所在圆O的半径为
m．
∴OE⊥AB，
∴AF=
| 1 |
| 2 |
| 3 |
| 2 |
∵
|
| AB |
∴AO=r，OF=r-1，
在Rt△AOF中，AO2=AF2+OF2，
即r2=（
| 3 |
| 2 |
解得r=
| 13 |
| 8 |
答：
|
| AB |
| 13 |
| 8 |
练习册系列答案
阅读快车系列答案
相关题目
