题目内容
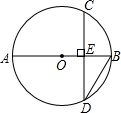
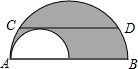
如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直径.

(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直径.

(1)证明:连接OC,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于E,
∴CE=ED,
=
.(2分)
∴∠BCD=∠BAC.(3分)
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD.(5分)
(2)设⊙O的半径为Rcm,则OE=OB-EB=(R-8)cm,
CE=
CD=
×24=12cm,(6分)
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R-8)2+122(8分)
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.(10分)
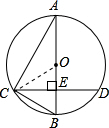
∵AB为⊙O的直径,CD是弦,且AB⊥CD于E,
∴CE=ED,
 |
| CB |
 |
| DB |
∴∠BCD=∠BAC.(3分)
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD.(5分)
(2)设⊙O的半径为Rcm,则OE=OB-EB=(R-8)cm,
CE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R-8)2+122(8分)
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.(10分)


练习册系列答案
相关题目