Question

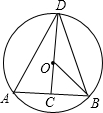
如图，已知AB是⊙O的弦，点C是弦AB上任意一点（不与点A．B重合），连接CO并延长CO交⊙O于点D，连接AD，DB．
（1）若∠OBC=38°，∠ADC=19°，求∠DOB的度数；
（2）若点C是AB的中点，⊙O的半径是4，AC=2

3

．求BD的长．

Answer 1

（1）连接OA，
∵OA=OD=OB，
∴∠DAO=∠ADC，∠OBC=∠OAB，
∵∠OBC=38°，∠ADC=19°，
∴∠DAO=19°，∠OAB=38°，
∴∠DAB=19°+38°=57°，
∴由圆周角定理得：∠DOB=2∠DAB=2×57°=114°．

（2）∵C为AB中点，OC过O，
∴DC⊥AB，BC=AC=2

3

，
∵OB=4，
∴在Rt△OCB中，由勾股定理得：OC=2，
即DC=OD+OC=4+2=6，
在Rt△DCB中，由勾股定理得：BD=

DC2+CB2

=

62+(2 3 )2

=4

3

．