题目内容
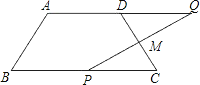
【题目】如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
(2)当点P在点B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.
【答案】(1)证明见解析;(2)PC=2,理由见解析.
【解析】试题分析: (1)要证明△PCM≌△QDM,可以根据两个三角形全等四个定理,即AAS、ASA、SAS、SSS中的ASA.利用∠QDM=∠PCM,DM=CM,∠DMQ=∠CMP即可得出;
(2)得出P在B、C之间运动的位置,根据一组对边平行且相等的四边形是平行四边形得出.
试题解析:
(1)∵AD∥BC,∴∠QDM=∠PCM.
∵M是CD的中点,∴DM=CM,∵∠DMQ=∠CMP,
在△PCM和△QDM中,∵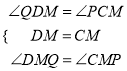 ,
,
∴△PCM≌△QDM(ASA).
(2)当四边形ABPQ是平行四边形时,PB=AQ,
∵BC﹣CP=AD+QD,∴9﹣CP=5+CP,∴CP=(9﹣5)÷2=2.
∴当PC=2时,四边形ABPQ是平行四边形.
点睛:本题中和考查全等三角形、平行四边形的判定,熟练掌握平行四边形的性质和判定方法是解题的关键.

练习册系列答案
相关题目