题目内容
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
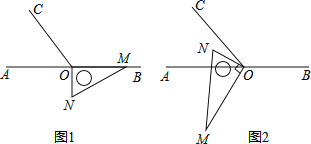
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)6、15、24、33.(2)∠AOM﹣∠NOC=30°,理由见解析
【解析】
试题分析:(1)根据已知条件可知,在第t秒时,三角板转过的角度为10°t,然后按照OA、OC、ON三条射线构成相等的角分四种情况讨论,即可求出t的值;
(2)根据三角板∠MON=90°可求出∠AOM、∠NOC和∠AON的关系,然后两角相加即可求出二者之间的数量关系.
解:(1)∵三角板绕点O按每秒10°的速度沿逆时针方向旋转,
∴第t秒时,三角板转过的角度为10°t,
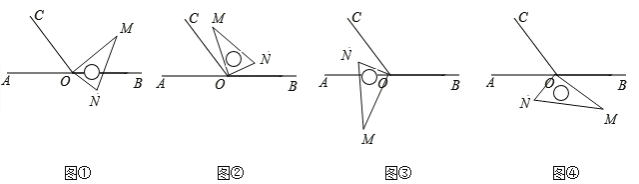
当三角板转到如图①所示时,∠AON=∠CON
∵∠AON=90°+10°t,∠CON=∠BOC+∠BON=120°+90°﹣10°t=210°﹣10°t
∴90°+10°t=210°﹣10°t
即t=6;
当三角板转到如图②所示时,∠AOC=∠CON=180°﹣120°=60°
∵∠CON=∠BOC﹣∠BON=120°﹣(10°t﹣90°)=210°﹣10°t
∴210°﹣10°t=60°
即t=15;
当三角板转到如图③所示时,∠AON=∠CON=![]() ,
,
∵∠CON=∠BON﹣∠BOC=(10°t﹣90°)﹣120°=10°t﹣210°
∴10°t﹣210°=30°
即t=24;
当三角板转到如图④所示时,∠AON=∠AOC=60°
∵∠AON=10°t﹣180°﹣90°=10°t﹣270°
∴10°t﹣270°=60°
即t=33.
故t的值为6、15、24、33.
(2)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案