Question

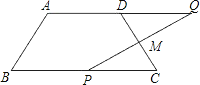
【题目】已知：如图，ABCD中，CD=CB=2，∠C=60°，点E是CD边上自D向C的动点（点E运动到点C停止运动），连结AE，以AE为一边作等边△AEP，连结DP．
（1）求证：△ABE≌△ADP；
（2）点P随点E的运动而运动，请直接写出点P的运动路径长 ．

Answer 1

【答案】
（1）证明：在ABCD中，

∵BC=CD，

∴ABCD是菱形，

∴AB=AD，

∵△AEP是等边三角形，

∴AP=AE，∠PAE=60°，

∵∠BAD=∠C=60°，

∴∠PAE=∠DAB，

∴∠PAE﹣∠DAE=∠DAB﹣∠DAE，

即∠1=∠2，

在△ABE与△ADP中，

，

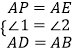∴△ABE≌△ADP（SAS）

（2）2
【解析】（2）解：∵点E在CD边上自D向C的运动， ∴点E的运动路径长是2，
∴点P的运动路径长为：2．
所以答案是：2．