题目内容
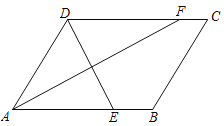
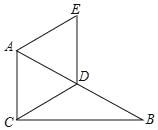
【题目】如图，已知Rt△ABC中，∠ACB＝90°，∠B＝30°，D是AB的中点，AE∥CD，AC∥ED，
求证：四边形ACDE是菱形．
【答案】证明见解析.
【解析】
由AE∥CD，AC∥ED可证四边形ACDE是平行四边形，
由直角三角形斜边上的中线等于斜边的一半可得CD＝
AB＝AD，
由∠ACB＝90°，∠B＝30°，可得∠CAB＝60°，即可证△ACD为等边三角形，由此可得AC＝CD，即可证平行四边形ACDE是菱形．
∵AE∥CD，AC∥ED，
∴四边形ACDE是平行四边形，
∵∠ACB＝90°，D为AB的中点，
∴CD＝AB＝AD，
∵∠ACB＝90°，∠B＝30°，
∴∠CAB＝60°，
∴△ACD为等边三角形，
∴AC＝CD，
∴平行四边形ACDE是菱形．
练习册系列答案
阅读快车系列答案
相关题目
