题目内容
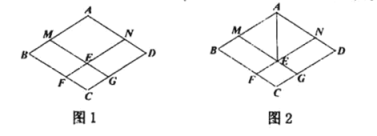
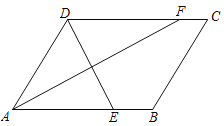
【题目】如图,平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点F,
于点F,![]() ,交
,交![]() 点
点![]() ,
,![]() ,则
,则![]() =_________.
=_________.
【答案】8
【解析】
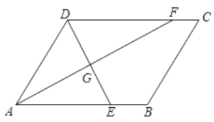
根据角平分线的定义和平行线的性质得:∠DFA=∠EAF=∠DAF,所以DF=AD=5,由等腰三角形三线合一的性质得:AG=FG,再证明AD=AE,可得DG=3,利用勾股定理得AG的长,可得结论.
解:如图,设AF,DE交于点G,
∵AF平分∠BAD,
∴∠DAF=∠EAF,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DFA=∠EAF=∠DAF,
∴DF=AD=5,
∵DE⊥AF,
∴AG=FG,
∵∠DAF=∠EAG,∠AGD=∠AGE,
∴∠ADE=∠AEG,
∴AE=AD=5,
∴DG=EG=![]() DE=
DE=![]() ×6=3,
×6=3,
由勾股定理得:AG=![]() ,
,
∴AF=2AG=8,
故答案为:8.

练习册系列答案
相关题目