Question

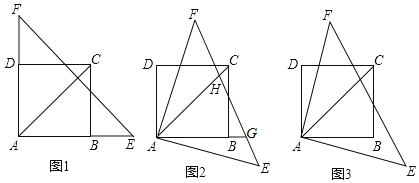
【题目】如图，平行四边形中，延长至使，连接交于点，点是线段的中点.

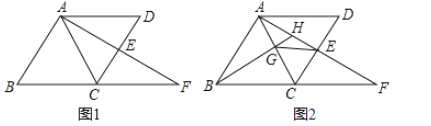
（1）如图1，若，，求平行四边形的面积；

（2）如图2，过点作交于点，于点，连接，若，求证：．

Answer 1

【答案】（1） （2）见解析

【解析】

（1）首先证明CE⊥AF，想办法求出CD，AE即可解决问题． （2）证明：如图2中，连接BE，作EK⊥AC于K．利用全等三角形的性质证明AG=EK=KG，即可解决问题．

（1）解：如图1中，

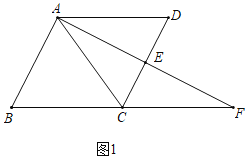
∵CA=CF，AE=EF， ∴CE⊥AF， ∵CE=1，∠F=30°，

∴CF=CA=2CE=2，AE=EF=，

∵四边形ABCD 平行四边形， ∴AD∥CF， ∴∠D=∠ECF，

∵∠AED=∠CEF，AE=EF， ∴△ADE≌△FCE（AAS），

∴CE=DE=1， ∴CD=2，

∴平行四边形ABCD的面积=CDAE=．

（2）证明：如图2中，连接BE，作EK⊥AC于K．

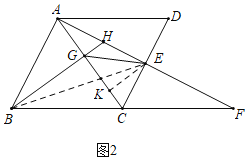
∵CE⊥AF，CE∥AB， ∴AB⊥AE，

∵BG⊥AC， ∴∠BAH=∠AEC=∠AGB=90°，

∴∠ABG+∠BAG=90°，∠BAG+∠CAE=90°，

∴∠ABH=∠CAE， ∵BH=AC， ∴△BAH≌△AEC（AAS），

∴BA=AE=CD，AH=CE=DE， ∴AB=2AH，

∵∠ABG=∠EAK，AB=AE，∠AGB=∠AKE，

∴△BGA≌△AKE（AAS）， ∴AG=EK，

∴tan∠ABH===，

∴tan∠EAK==， ∴AK=2EK， ∴AG=GK， ∴KG=KE，

∵∠EKG=90°， ∴EG==．