题目内容
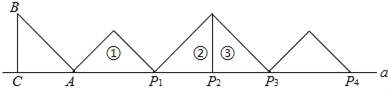
【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
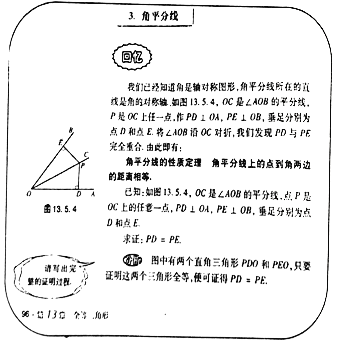

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
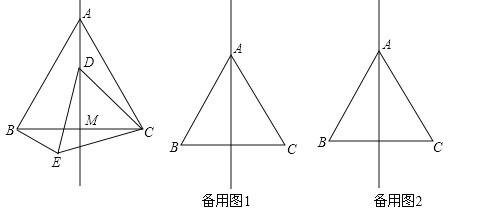
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
【答案】教材呈现:见解析;定理应用:(1)见解析;(2)3
【解析】
教材呈现:
利用AAS可证明△POD≌△POE(AAS),即可得出PD=PE;
定理应用:
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,由角平分线的性质定理可得EF=EG=EH,利用AAS可证明△BEF≌△CEH,得出BE=EC;
(2)利用HL可证明Rt△AEF≌Rt△AEG,得出AF=AG,同理DG=DH,由(1)得出△BEF≌△CEH,得出BF=CH,设BF=CH=x,AF=AG=y,DG=DH=z,由四边形ABCD的周长得出x+y+z=10,由四边形ABCD的面积得出(x+y+z)EF=30,求出EF=3即可.
教材呈现:角平分线的性质定理:角平分线上的点到角两边的距离相等.
已知:OC是∠AOB的平分线,点P是OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别是点D和E.
求证:PD=PE.
证明:∵OC是∠AOB的平分线,
∴∠POD=∠POE,
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△POD和△POE中, ,
,
∴△POD≌△POE(AAS),
∴PD=PE.
定理应用:
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在△BEF与△CEH中, ,
,
∴△BEF≌△CEH(AAS),
∴BE=CE.

(2)解:∵EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在Rt△AEF和Rt△AEG中,![]() ,
,
∴Rt△AEF≌Rt△AEG(HL),
∴AF=AG,
同理:DG=DH,
由(1)得:△BEF≌△CEH,
∴BF=CH,
设BF=CH=x,AF=AG=y,DG=DH=z,
∵四边形ABCD的周长为24,CE=BE=2,
∴x+y+y+z+z+x+2+2=24,
∴x+y+z=10,
∵四边形ABCD的面积为30,
∴![]() (x+y)EF+
(x+y)EF+![]() (y+z)EG+
(y+z)EG+![]() (z+x)ED=30,
(z+x)ED=30,
整理得:(x+y+z)EF=30,即10×EF=30,
∴EF=3,
即△ABE的边AB的高的长为3.
故答案为:3