题目内容
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(其中
两点(其中![]() 为坐标原点),过点
为坐标原点),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() (其中
(其中![]() 、
、![]() 不重合),连接
不重合),连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 和
和![]() .
.
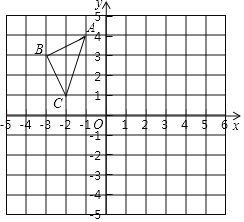
(1)![]() 时,求抛物线的解析式和
时,求抛物线的解析式和![]() 的长;
的长;
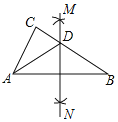
![]() 如图
如图![]() 时,若
时,若![]() ,求
,求![]() 的值.
的值.

【答案】![]()
![]() ,∴
,∴![]() ;
;![]()
![]() .
.
【解析】
(1)令a=![]() 代入抛物线,由于抛物线过原点,所以b=0,从而求出抛物线的解析式,然后根据条件求出点B与C的坐标即可求出BC的长度.
代入抛物线,由于抛物线过原点,所以b=0,从而求出抛物线的解析式,然后根据条件求出点B与C的坐标即可求出BC的长度.
(2)由题意可知b=0,然后根据P的坐标分别求出A、B、C、M的坐标,进而求出BC、BP、PM、AM的长度,最后利用△AMP∽△BPC列出关于a的方程即可求出a的值.
![]() 当
当![]() 时,
时,
∴抛物线为:![]() ,
,
∴对称轴为![]() ,
,
又∵抛物线过原点,
∴![]() ,
,
∴![]() ,
,
∴令![]() 代入
代入![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() 由于抛物线过原点
由于抛物线过原点![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() 代入
代入![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∵点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,
,
抛物线的对称轴为![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目