题目内容
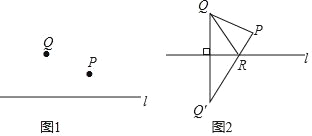
【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
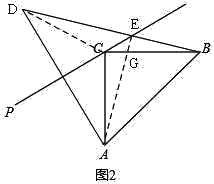
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

【答案】(1)①见解析;②30°;(2)DE2+BE2=2AC2,理由见解析
【解析】
(1)根据题意作图,进而求∠CBD的度数(2)由45°<∠ACP<90°,根据题意和图形可得DE2+BE2=2AC2 .
(1)如图1所示,
(2)如图1,连接CD,
∵点A关于直线CP的对称点为D,
∴CP是AD的垂直平分线,
∴CD=AC,∠DCP=∠ACP=15°,
∵∠ACB=90°,
∴∠BCD=90°+15°+15°=120°,
∵AC=BC=CD,
∴∠CBD=∠CDB=30°,
(3)DE2+BE2=2AC2,
理由是:如图2,连接CD、AE,
∵DC=BC=AC,
∴∠CDB=∠CBD=∠CAE,
∵∠CGA=∠EGB,
∴∠GEB=∠ACB=90°,
∴AE2+BE2=AB2,
∵CP是AD的垂直平分线,
∴ED=AE,
∴DE2+BE2=AB2,
∵△ABC是等腰直角三角形,
∴AB2=AC2+BC2,且AC=BC,
∴DE2+BE2=2AC2.

练习册系列答案
相关题目