��Ŀ����
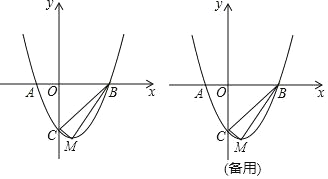
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c�Ķ�������Ϊ��2��9������y�ύ�ڵ�A��0��5������x�ύ�ڵ�E��B��
��1������κ���y=ax2+bx+c�ı���ʽ��
��2������A��ACƽ����x�ᣬ���������ڵ�C����PΪ�������ϵ�һ�㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D���ʵ���P�ں�λ��ʱ���ı���APCD�������������������
��3������M���������ϣ���N����Գ����ϣ�ʹ����A��E��N��MΪ������ı�����ƽ���ı��Σ���AEΪ��һ�ߣ����M��N�����꣮

���𰸡���1��y=��x2+4x+5����2����P��![]() ��
��![]() ��ʱ��S�ı���APCD���=
��ʱ��S�ı���APCD���=![]() ����3����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13������M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����
����3����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13������M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����
��������
���⣨1����������߽���ʽ���ô���ϵ������⼴�ɣ���2�������ֱ��AB����ʽ�������P���꣨x����x2+4x+5��������������ϵʽS�ı���APCD=��2x2+10x�����ݶ��κ��������ֵ����3�����жϳ���HMN�ա�AOE�����M��ĺ����꣬�Ӷ������M��N�����꣮
�����������1���������߽���ʽΪy=a![]() +9������������y�ύ�ڵ�A��0��5���� ��4a+9=5��
+9������������y�ύ�ڵ�A��0��5���� ��4a+9=5��
��a=��1�� y=��![]() +9=-
+9=-![]() +4x+5��
+4x+5��
��2����y=0ʱ��-![]() +4x+5=0����x1=��1��x2=5����E����1��0����B��5��0����
+4x+5=0����x1=��1��x2=5����E����1��0����B��5��0����
��ֱ��AB�Ľ���ʽΪy=mx+n����A��0��5����B��5��0������m=��1��n=5��
��ֱ��AB�Ľ���ʽΪy=��x+5����P��x����![]() +4x+5���� ��D��x����x+5����
+4x+5���� ��D��x����x+5����
��PD=-![]() +4x+5+x��5=-
+4x+5+x��5=-![]() +5x�� ��AC=4�� ��S�ı���APCD=
+5x�� ��AC=4�� ��S�ı���APCD=![]() ��AC��PD=2��-
��AC��PD=2��-![]() +5x��=-2
+5x��=-2![]() +10x��
+10x��
����x=![]() ʱ�� ��S�ı���APCD���=
ʱ�� ��S�ı���APCD���=![]() ��
��
��3����ͼ��
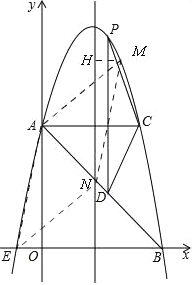
��M��MH��ֱ�ڶԳ��ᣬ����ΪH����MN��AE��MN=AE�����HMN�ա�AOE����HM=OE=1��
��M��ĺ�����Ϊx=3��x=1����x=1ʱ��M��������Ϊ8����x=3ʱ��M��������Ϊ8��
��M�������ΪM1��1��8����M2��3��8������A��0��5����E/span>����1��0���� ��ֱ��AE����ʽΪy=5x+5��
��MN��AE����MN�Ľ���ʽΪy=5x+b������N�������߶Գ���x=2�ϣ���N��2��10+b����
��AE2=OA2+0E2=26 ��MN=AE ��MN2=AE2�� ��MN2=��2��1��2+[8����10+b��]2=1+��b+2��2
��M�������ΪM1��1��8����M2��3��8���� ����M1��M2���������߶Գ���x=2�Գƣ�
����N�������߶Գ����ϣ� ��M1N=M2N�� ��1+��b+2��2=26�� ��b=3����b=��7��
��10+b=13��10+b=3 ����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13����
��M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�