题目内容
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
【答案】
(1)
解:由题意A(﹣2,5),对称轴x=﹣ ![]() =4,
=4,
∵A、B关于对称轴对称,
∴B(10,5).
(2)
解:①如图1中,
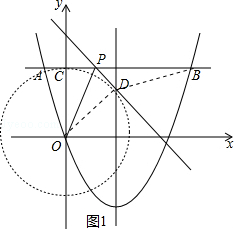
由题意点D在以O为圆心OC为半径的圆上,
∴当O、D、B共线时,BD的最小值=OB﹣OD= ![]() ﹣5=5
﹣5=5 ![]() ﹣5.
﹣5.
②如图中,
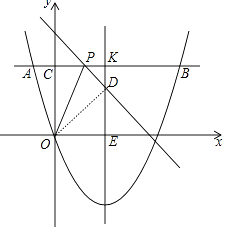
当点D在对称轴上时,在Rt△ODE中,OD=OC=5,OE=4,
∴DE= ![]() =
= ![]() =3,
=3,
∴点D的坐标为(4,3).
设PC=PD=x,在Rt△PDK中,x2=(4﹣x)2+22,
∴x= ![]() ,
,
∴P( ![]() ,5),
,5),
∴直线PD的解析式为y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)思想确定点A的坐标,利用对称轴公式求出对称轴,再根据对称性可得点B坐标;(2)①由题意点D在以O为圆心OC为半径的圆上,推出当O、D、B共线时,BD的最小值=OB﹣OD;②当点D在对称轴上时,在Rt△OD=OC=5,OE=4,可得DE= ![]() =
= ![]() =3,求出P、D的坐标即可解决问题;
=3,求出P、D的坐标即可解决问题;
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目